
30 August 2024
Asteroids, those ancient wanderers of our solar system, have long captivated astronomers and space scientists. Of course, the asteroids hold the key to unravelling the mysteries of our cosmic origins. But beyond that, these celestial bodies present unique opportunities for space exploration, and they do have some rare elements we would like to mine and take.
When it comes to exploring asteroids, finding the right orbits for spacecraft is crucial. Periodic orbits around these celestial bodies are potential trajectories for space probes, mining facilities, and even deep space stations. A periodic orbit is a closed, repeating trajectory in the asteroid’s rotating reference frame – like satellite trajectories around Earth. A periodic orbit family is a group of related periodic orbits with similar characteristics, such as shape, but may differ in size.
While various periodic orbit families and their bifurcations around asteroids have been extensively studied, a specific type of bifurcation, known as period-multiplying bifurcations, has received less attention. In his research published in Aerospace, Rishi—my PhD student—focused on computing these elusive period-multiplying bifurcations of periodic orbit families around asteroids.
What are period-multiplying bifurcations, you ask? Even before that, ‘What are bifurcations of periodic orbit families?’
Starting from a periodic orbit that belongs to a family, we can compute another member of the same family (having a similar shape but a little bigger, maybe) using a numerical technique called continuation. Now, from this new member, we can compute a little more bigger orbit, and so on. However, as we progress, sometimes, we encounter situations where the nature or stability of orbits in a family change dramatically. At these points, new families of periodic orbits can emerge from or merge with existing families. These events are called as bifurcations of periodic orbits. These are consequences of the complex gravitational field around asteroids.
Period-multiplying bifurcations are the ones where, from a periodic orbit, a new family emerges such that the member of the new family has a period that is an integer multiple of the period of the orbit from which it bifurcated. In the existing literature, studying period-multiplying bifurcations around asteroids has, until now, received scarce attention.
But why is this important? Calculating these high-period orbits not only expands our knowledge of potential trajectories for asteroid exploration but also provides insights into simulating long-duration trajectories around asteroids – a crucial aspect for future space missions.
Traditionally, researchers have relied on single-shooting and multiple-shooting methods to compute bifurcations of periodic orbit families. However, Rishi encountered computational difficulties when applying these methods to period-multiplying bifurcations. This led him to explore an alternative approach: the Legendre–Gauss collocation method.
By employing this collocation method, Rishi overcame the limitations of shooting methods and successfully computed the period-multiplying bifurcations around the asteroid 216 Kleopatra. Using the proposed computational technique, he successfully obtained orbits with periods approximately 7 and 17 times the rotational period of this asteroid. In a broader context, this study demonstrates the effectiveness of collocation techniques in solving orbital mechanics problems around asteroids, particularly when dealing with long-duration orbits.
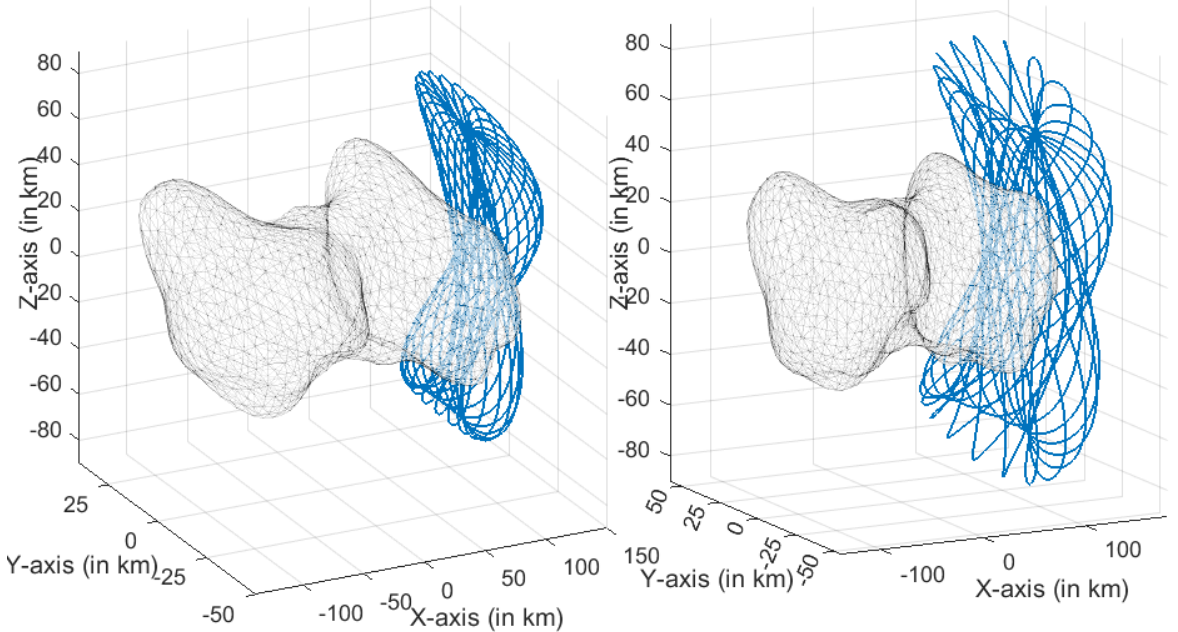 Examples of computed period-17 orbits that bifurcated from a simple 8-shaped orbit. The coverage of the high-period orbits is substantially larger than that of the parent orbit, making these useful for asteroid exploration.
Examples of computed period-17 orbits that bifurcated from a simple 8-shaped orbit. The coverage of the high-period orbits is substantially larger than that of the parent orbit, making these useful for asteroid exploration.
The implications of Rishi’s work extend beyond just the asteroid Kleopatra. The proposed methods can be applied to other asteroids, opening up new possibilities for space exploration and asteroid mining missions. Imagine spacecraft following intricate, high-period orbits that maximise coverage or enable efficient resource extraction.
Future work will involve stability analyses of these computed high-period orbits, as well as the potential discovery of even more stable orbits compared to the parent families.